Energi Potensial
Energi potensial merupakan energi yang dihubungkan dengan gaya-gaya yang bergantung pada posisi atau wujud benda dan lingkungannya. Banyak sekali contoh energi potensial dalam kehidupan kita. Karet ketapel yang kita regangkan memiliki energi potensial. Karet ketapel dapat melontarkan batu karena adanya energi potensial pada karet yang diregangkan. Demikian juga busur yang ditarik oleh pemanah dapat menggerakan anak panah, karena terdapat energi potensial pada busur yang diregangkan. Contoh lain adaah pegas yang ditekan atau diregangkan. Energi potensial pada tiga contoh ini disebut senergi potensial elastik. Energi kimia pada makanan yang kita makan atau energi kimia pada bahan bakar juga termasuk energi potensial. Ketika makanan di makan atau bahan bakar mengalami pembakaran, baru energi kimia yang terdapat pada makanan atau bahan bakar tersebut dapat dimanfaatkan. Energi magnet juga termasuk energi potensial. Ketika kita memegang sesuatu yang terbuat dari besi di dekat magnet, pada benda tersebut sebenarnya bekerja energi potensial magnet. Ketika kita melepaskan benda yang kita pegang (paku, misalnya), dalam waktu singkat paku tersebut bergerak menuju magnet dan menempel pada magnet. Perlu dipahami bahwa paku memiliki energi potensial magnet ketika berada jarak tertentu dari magnet; ketika menempel pada magnet, energi potensial bernilai nol.
Energi Potensial Gravitasi
Contoh yang paling umum dari energi potensial adalah energi potensial gravitasi. Buah mangga yang lezat dan ranum memiliki energi potensial gravitasi ketika sedang menggelayut pada tangkainya. Demikian juga ketika anda berada pada ketinggian tertentu dari permukaan tanah (misalnya di atap rumah  atau di dalam pesawat). Energi potensial gravitasi dimiliki benda karena posisi relatifnya terhadap bumi. Setiap benda yang memiliki energi potensial gravitasi dapat melakukan kerja apabila benda tersebut bergerak menuju permukaan bumi (misalnya buah mangga jatuh dari pohon). Untuk memudahkan pemahamanmu, lakukan percobaan sederhana berikut ini. Pancangkan sebuah paku di tanah. Angkatlah sebuah batu yang ukurannya agak besar dan jatuhkan batu tegak lurus pada paku tersebut. Amati bahwa paku tersebut terpancang semakin dalam akibat usaha alias kerja yang dilakukan oleh batu yang anda jatuhkan.
atau di dalam pesawat). Energi potensial gravitasi dimiliki benda karena posisi relatifnya terhadap bumi. Setiap benda yang memiliki energi potensial gravitasi dapat melakukan kerja apabila benda tersebut bergerak menuju permukaan bumi (misalnya buah mangga jatuh dari pohon). Untuk memudahkan pemahamanmu, lakukan percobaan sederhana berikut ini. Pancangkan sebuah paku di tanah. Angkatlah sebuah batu yang ukurannya agak besar dan jatuhkan batu tegak lurus pada paku tersebut. Amati bahwa paku tersebut terpancang semakin dalam akibat usaha alias kerja yang dilakukan oleh batu yang anda jatuhkan.
Sekarang mari kita tentukan besar energi potensial gravitasi sebuah benda di dekat permukaan bumi. Misalnya kita mengangkat sebuah batu bermassa m. gaya angkat yang kita berikan pada batu paling tidak sama dengan gaya berat yang bekerja pada batu tersebut, yakni mg (massa kali percepatan gravitasi). Untuk mengangkat batu dari permukaan tanah hingga mencapai ketinggian h, maka kita harus melakukan usaha yang besarnya sama dengan hasil kali gaya berat batu (W = mg) dengan ketinggian h. Ingat ya, arah gaya angkat kita sejajar dengan arah perpindahan batu, yakni ke atas… FA = gaya angkat
W = FA . s = (m)(-g) (s) = – mg(h2-h1) —– persamaan 1
Tanda negatif menunjukkan bahwa arah percepatan gravitasi menuju ke bawah…

Dengan demikian, energi potensial gravitasi sebuah benda merupakan hasil kali gaya berat benda (mg) dan ketinggiannya (h). h = h2 – h1
EP = mgh —— persamaan 2
Berdasarkan persamaan EP di atas, tampak bahwa makin tinggi (h) benda di atas permukaan tanah, makin besar EP yang dimiliki benda tersebut. Ingat ya, EP gravitasi bergantung pada jarak vertikal alias ketinggian benda di atas titik acuan tertentu. Biasanya kita tetapkan tanah sebagai titik acuan jika benda mulai bergerak dari permukaan tanah atau gerakan benda menuju permukaan tanah. Apabila kita memegang sebuah buku pada ketinggian tertentu di atas meja, kita bisa memilih meja sebagai titik acuan atau kita juga bisa menentukan permukaan lantai sebagai titik acuan. Jika kita tetapkan permukaan meja sebagai titik acuan maka h alias ketinggian buku kita ukur dari permukaan meja. Apabila kita tetapkan tanah sebagai titik acuan maka ketinggian buku (h) kita ukur dari permukaan lantai.
Jika kita gabungkan persamaan 1 dengan persamaan 2 :

Persamaan ini menyatakan bahwa usaha yang dilakukan oleh gaya yang menggerakan benda dari h1 ke h2 (tanpa percepatan) sama dengan perubahan energi potensial benda antara h1 dan h2. Setiap bentuk energi potensial memiliki hubungan dengan suatu gaya tertentu dan dapat dinyatakan sama dengan EP gravitasi. Secara umum, perubahan EP yang memiliki hubungan dengan suatu gaya tertentu, sama dengan usaha yang dilakukan gaya jika benda dipindahkan dari kedudukan pertama ke kedudukan kedua. Dalam makna yang lebih sempit, bisa dinyatakan bahwa perubahan EP merupakan usaha yang diperlukan oleh suatu gaya luar untuk memindahkan benda antara dua titik, tanpa percepatan.
Contoh soal 1 :
Buah mangga yang ranum dan mengundang selera menggelayut pada tangkai pohon mangga yang berjarak 10 meter dari permukaan tanah. Jika massa buah mangga tersebut 0,2 kg, berapakah energi potensialnya ? anggap saja percepatan gravitasi 10 m/s2.
Panduan jawaban :
EP = mgh
EP = (0,2 kg) (10 m/s2) (10 m)
EP = 20 Kg m2/s2 = 20 N.m = 20 Joule
Contoh soal 2 :
Seekor monyet bermassa 5 kg berayun dari satu dahan ke dahan lain yang lebih tinggi 2 meter. Berapakah perubahan energi potensial monyet tersebut ? g = 10 m/s2
Panduan jawaban :
Soal ini sangat gampang… kita tetapkan dahan pertama sebagai titik acuan, di mana h = 0. Kita hanya perlu menghitung EP monyet ketika berada pada dahan kedua…
EP = mgh = (5 kg) (10 m/s2) (2 m)
EP = 100 Joule
Dengan demikian, perubahan energi potensial monyet = 100 Joule.
Contoh soal 3 :
Seorang buruh pelabuhan yang tingginya 1,50 meter mengangkat sekarung beras yang bermassa 50 kg dari permukaan tanah dan memberikan kepada seorang temannya yang berdiri di atas kapal. Jika orang tersebut tersebut berada 0,5 meter tepat di atas kepala buruh pelabuhan, hitunglah energi potensial karung berisi beras relatif terhadap :
a) permukaan tanah
b) kepala buruh pelabuhan
Panduan jawaban :
a). EP karung berisi beras relatif terhadap permukaan tanah
Ketinggian total karung beras dari permukaan tanah = 1,5 m + 0,5 m = 2 meter
Dengan demikian,
EP = mgh = (50 kg) (10 m/s2) (2 m)
EP = 1000 Joule
b). EP karung berisi beras relatif terhadap kepala buruh pelabuhan
Kedudukan karung beras diukur dari kepala buruh pelabuhan adalah 0,5 meter.
EP = mgh = (50 kg) (10 m/s2) (0,5 m)
EP = 250 Joule
Energi Potensial Elastis
Sebagaimana dijelaskan pada bagian awal tulisan ini, selain energi potensial gravitasi terdapat juga energi potensial elastis. EP elestis berhubungan dengan benda-benda yang elastis, misalnya pegas. Mari kita bayangkan sebuah pegas yang ditekan dengan tangan. Apabila kita melepaskan tekanan pada pegas, maka pegas tersebut melakukan usaha pada tangan kita. Efek yang dirasakan adalah tangan kita terasa seperti di dorong. Apabila kita menempelkan sebuah benda pada ujung pegas, kemudian pegas tersebut kita tekan, maka setelah dilepaskan benda yang berada di ujung pegas pasti terlempar…. perhatikan gambar di bawah. Jika dirimu mempunyai koleksi pegas, baik di rumah maupun di sekolah, silahkan melakukan percobaan ini untuk membuktikannya….

Ketika berada dalam keadaan diam, setiap pegas memiliki panjang alami, seperti ditunjukkan gambar a (lihat gambar di bawah). Jika pegas di tekan sejauh x dari panjang alami, diperlukan gaya sebesar FT (gaya tekan) yang nilainya berbanding lurus dengan x, yakni :
FT = kx

k adalah konstanta pegas (ukuran kelenturan/elastisitas pegas) dan besarnya tetap. Ketika ditekan, pegas memberikan gaya reaksi, yang besarnya sama dengan gaya tekan tetapi arahnya berlawanan. gaya reaksi pegas tersebut dikenal sebagai gaya pemulih. Besarnya gaya pemulih adalah :
FP = -kx
Tanda minus menunjukkan bahwa arah gaya pemulih berlawanan arah dengan gaya tekan. Ini adalah persamaan hukum Hooke. Persamaan ini berlaku apabila pegas tidak ditekan sampai melewati batas elastisitasnya (x tidak sangat besar).
Untuk menghitung Energi Potensial pegas yang ditekan atau diregangkan, terlebih dahulu kita hitung gaya usaha yang diperlukan untuk menekan atau meregangkan pegas. Kita tidak bisa menggunakan persamaan W = F s = F x, karena gaya tekan atau gaya regang yang kita berikan pada pegas selalu berubah-ubah selama pegas ditekan. Ketika menekan pegas misalnya, semakin besar x, gaya tekan kita juga semakin besar. Beda dengan gaya angkat yang besarnya tetap ketika kita mengangkat batu. Lalu bagaimana cara mengakalinya ?
Kita menggunakan gaya rata-rata. Gaya tekan atau gaya regang selalu berubah, dari F = 0 ketika x = 0 sampai F = kx (ketika pegas tertekan atau teregang sejauh x). Besar gaya rata-rata adalah :

x merupakan jarak total pegas yang teregang atau pegas yang tertekan (bandingkan dengan gambar di atas).
Usaha yang dilakukan adalah :

Nah, akhirnya kita menemukan persamaan Energi Potensial elastis (EP Pegas)….

Catatan :
Tidak ada rumus umum untuk Energi Potensial. Berbeda dengan energi kinetik yang memiliki satu rumus umum, EK = ½ mv2, bentuk persamaan EP bergantung gaya yang melakukan usaha… kalo bingung berlanjut, silahkan pelajari kembali ya…. sampai teler 
Sekarang, mari kita pelajari pokok bahasan Energi Kinetik….
Istirahat dulu, masa ga teller dari tadi pelototin terus ne tulisan  pisss……
pisss……
Energi Kinetik
Setiap benda yang bergerak memiliki energi. Ketapel yang ditarik lalu dilepaskan sehingga batu yang berada di dalam ketapel meluncur dengan kecepatan tertentu. Batu yang bergerak tersebut memiliki energi. Jika diarahkan pada ayam tetangga maka kemungkinan besar ayam tersebut lemas tak berdaya akibat dihajar batu. Pada contoh ini batu melakukan kerja pada ayam  Kendaraan beroda yang bergerak dengan laju tertentu di jalan raya juga memiliki energi kinetik. Ketika dua buah kendaraan yang sedang bergerak saling bertabrakan, maka bisa dipastikan kendaraan akan digiring ke bengkel untuk diperbaiki. Kerusakan akibat tabrakan terjadi karena kedua mobil yang pada mulanya bergerak melakukan usaha / kerja satu terhadap lainnya. Ketika tukang bangunan memukul paku menggunakan martil, martil yang digerakan tukang bangunan melakukan kerja pada paku.
Kendaraan beroda yang bergerak dengan laju tertentu di jalan raya juga memiliki energi kinetik. Ketika dua buah kendaraan yang sedang bergerak saling bertabrakan, maka bisa dipastikan kendaraan akan digiring ke bengkel untuk diperbaiki. Kerusakan akibat tabrakan terjadi karena kedua mobil yang pada mulanya bergerak melakukan usaha / kerja satu terhadap lainnya. Ketika tukang bangunan memukul paku menggunakan martil, martil yang digerakan tukang bangunan melakukan kerja pada paku.
Setiap benda yang bergerak memberikan gaya pada benda lain dan memindahkannya sejauh jarak tertentu. Benda yang bergerak memiliki kemampuan untuk melakukan kerja, karenanya dapat dikatakan memiliki energi. Energi pada benda yang bergerak disebut energi kinetik. Kata kinetik berasal dari bahasa yunani, kinetikos, yang artinya “gerak”. ketika benda bergerak, benda pasti memiliki kecepatan. Dengan demikian, kita dapat menyimpulkan bahwa energi kinetik merupakan energi yang dimiliki benda karena gerakannya atau kecepatannya.
Sekarang mari kita turunkan persamaan Energi Kinetik.
Untuk menurunkan persamaan energi kinetik, bayangkanlah sebuah benda bermassa m sedang bergerak pada lintasan lurus dengan laju awal vo.

Agar benda dipercepat beraturan sampai bergerak dengan laju v maka pada benda tersebut harus diberikan gaya total yang konstan dan searah dengan arah gerak benda sejauh s. Untuk itu dilakukan usaha alias kerja pada benda tersebut sebesar W = F s. Besar gaya F = m a.
Karena benda memiliki laju awal vo, laju akhir vt dan bergerak sejauh s, maka untuk menghitung nilai percepatan a, kita menggunakan persamaan vt2 = vo2 + 2as.

Kita subtitusikan nilai percepatan a ke dalam persamaan gaya F = m a, untuk menentukan besar usaha :

Persamaan ini menjelaskan usaha total yang dikerjakan pada benda. Karena W = EK maka kita dapat menyimpulkan bahwa besar energi kinetik translasi pada benda tersebut adalah :
W = EK = ½ mv2 —– persamaan 2
Persamaan 1 di atas dapat kita tulis kembali menjadi :

Persamaan 3 menyatakan bahwa usaha total yang bekerja pada sebuah benda sama dengan perubahan energi kinetiknya. Pernyataan ini merupakan prinsip usaha-energi. Prinsip usaha-energi berlaku jika W adalah usaha total yang dilakukan oleh setiap gaya yang bekerja pada benda. Jika usaha positif (W) bekerja pada suatu benda, maka energi kinetiknya bertambah sesuai dengan besar usaha positif tersebut (W). Jika usaha (W) yang dilakukan pada benda bernilai negatif, maka energi kinetik benda tersebut berkurang sebesar W. Dapat dikatakan bahwa gaya total yang diberikan pada benda di mana arahnya berlawanan dengan arah gerak benda, maka gaya total tersebut mengurangi laju dan energi kinetik benda. Jika besar usaha total yang dilakukan pada benda adalah nol, maka besar energi kinetik benda tetap (laju benda konstan).
Contoh soal 1 :
Sebuah bola sepak bermassa 150 gram ditendang oleh Ronaldo dan bola tersebut bergerak lurus menuju gawang dengan laju 30 m/s. Hitunglah :
a) energi kinetik bola tersebut
b) berapa usaha yang dilakukan Ronaldo pada bola untuk mencapai laju ini, jika bola mulai bergerak dari keadaan diam ?
panduan jawaban :
a) Energi Kinetik bola
EK= ½ mv2 = ½ (0,15 kg) (30 m/s2)2 = 67,5 Joule
b) Usaha total
W = EK2 – EK1
EK2 = 67,5 Joule
EK1 = ½ mv2 = ½ m (0) = 0 — laju awal bola (vo) = 0
Dengan demikian, usaha total :
W = 67,5 Joule – 0 = 67,5 Joule
Contoh soal 2 :
Berapa usaha yang diperlukan untuk mempercepat gerak sepeda motor bermassa 200 kg dari 5 m/s sampai 20 m/s ?
Panduan jawaban :
Pertanyaan soal di atas adalah berapa usaha total yang diperlukan untuk mempercepat gerak motor.
W = EK2 – EK1
Sekarang kita hitung terlebih dahulu EK1 dan EK2
EK1 = ½ mv12 = ½ (200 kg) (5 m/s)2 = 2500 J
EK2 = ½ mv22 = ½ (200 kg) (20 m/s)2 = 40.000 J
Energi total :
W = 40.000 J – 2.500 J
W = 37.500 J
Referensi :
Giancoli, Douglas C., 2001, Fisika Jilid I (terjemahan), Jakarta : Penerbit Erlangga
Halliday dan Resnick, 1991, Fisika Jilid I, Terjemahan, Jakarta : Penerbit Erlangga
Tipler, P.A.,1998, Fisika untuk Sains dan Teknik-Jilid I (terjemahan), Jakarta : Penebit Erlangga
Young, Hugh D. & Freedman, Roger A., 2002, Fisika Universitas (terjemahan), Jakarta : Penerbit Erlangga


 Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.
Gas dikatakan melakukan usaha apabila volume gas bertambah besar (atau mengembang) dan V2 > V1. sebaliknya, gas dikatakan menerima usaha (atau usaha dilakukan terhadap gas) apabila volume gas mengecil atau V2 < V1 dan usaha gas bernilai negatif.










 dapat dituliskan sebagai
dapat dituliskan sebagai 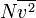 , di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan
, di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan  di mana
di mana 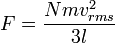

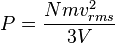

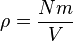 .
.
 yakni suatu sifat
yakni suatu sifat 
 (2)
(2)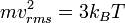

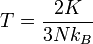 (3)
(3) (4)
(4)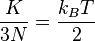 (5)
(5)